Итальянский математик создал несколько сложных формул, которые могут объяснить кривую вращения спиральной галактики не прибегая к помощи темной материи.
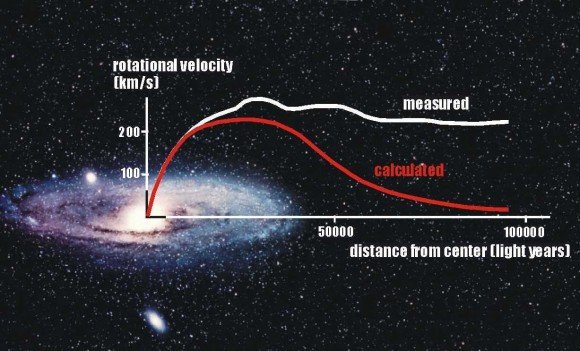
В настоящее время эти кривые вращения представляют собой ключевые доказательства существования темной материи. Звезды, рассыпанные по краям галактик, движутся так быстро, что они должны улететь в межгалактическое пространство. Но раз этого не происходит, то предполагается наличие дополнительной “невидимой” массы (темной материи), которая способна гравитационно удерживать их на своих орбитах.
В качестве примера можно рассмотреть кеплеровское движение планет в нашей Солнечной системе. Меркурий обращается вокруг Солнца с орбитальной скоростью 48 километров в секунду, в то время как Нептун вращается вокруг Солнца с орбитальной скоростью 5 километров в секунду. В солнечной системе расстояние от планеты до значительной массы Солнца зависит от ее орбитальной скорости. Таким образом, гипотетически, если бы масса Солнца была каким-то образом снижена, существующая орбитальная скорость Нептуна переместила бы его с текущей орбиты во вне, то есть в межзвездное пространство (если изменения были бы достаточно существенными).
Физика галактики Млечный Путь отличается от Солнечной системы, так как ее масса распределена более равномерно по всему галактическому диску, а в случае с Солнечной системой 99% массы сосредоточены в центре.
Тем не менее, если предположить подобные отношения между кумулятивной массой Млечного Пути и орбитальной скоростью его наиболее удаленных звезд, мы должны признать, что видимые объекты в пределах Млечного Пути – это только 10-20% массы, которая необходима для сдерживания орбитальной скорости звезд в его внешнем диске. Таким образом, мы приходим к тому, что остальная часть массы галактики должна быть темной (невидимой) материей.
Этот современный взгляд на то, как устроены и “работают” галактики является ключевым компонентом текущей стандартной космологической модели Вселенной. Однако Карати (A. Carati) предположил невероятную, казалось бы, идею, что кривые вращения спиральных галактик можно объяснять гравитационным влиянием далекой материи, не прибегая к помощи темной материи вообще.
Концептуально идея не имеет смысла. Нахождение значительной гравитационной массы за пределами орбиты звезд могло бы вытянуть их на более широкие орбиты, но трудно понять, почему это прибавило бы им орбитальной скорости. Вовлечение объектов в более широкую орбиту должно привести к тому, что орбита будет занимать больше времени, поскольку она будет иметь большую окружность. Однако то, что мы обычно видим в спиральных галактиках – звезды на удаленной орбите проходят ее за такой же период времени, что и более близкие к центру звезды.
Но, несмотря на то, что предложенный механизм кажется немного неправдоподобным, особенно поражает в утверждении Карати то, что математика по-видимому смогла дать описание кривых вращения галактик, которое подходит под наблюдаемые значения как минимум четырех известных галактик.
Математика опирается на принципы, установленные в уравнениях поля Эйнштейна, что и является проблематичным, поскольку уравнения поля основаны на космологическом принципе, который предполагает, что воздействие далекой материи незначительно.
Интересно, в статье Карати приводится два примера такого воздействия. С одной стороны воздействие удаленной материи состоит в том, что она вызывает положительное давление, которое обеспечивает быстрое движение звезд, препятствуя их разлету; а с другой стороны – она может вызвать отрицательное давление, которое ведет к нетипичному распаду кривой вращения галактики.
Подробнее в “Carati Gravitational effects of the faraway matter on the rotation curves of spiral galaxies”